6.5 Applications to Physics: Velocity, Distance, Work and Energy
In this section we will see how Calculus can be applied to the concepts of velocity, distance, work and energy.
6.5.1 Velocity and Distance
We can think of an antiderivative as a solution to the differential equation
\[ \frac{dy}{dx} = f(x) \tag{2} \]
An initial condition is like the \(y\)-intercept of a line, which determines one particular line among all lines with the same slope. The graphs of the antiderivatives of \(f(x)\) are all parallel (see Figure 5.28 in Section 5.3), and the initial condition determines one of them.
In general, a differential equation is an equation relating an unknown function and its derivatives. The unknown in Eq. (2) is a function \(y = F(x)\) whose derivative is \(f(x)\); that is, \(F(x)\) is an antiderivative of \(f(x)\).
Eq. (2) has infinitely many solutions (because the antiderivative is not unique), but we can specify a particular solution by imposing an initial condition—that is, by requiring that the solution satisfy \(y(x_{0}) = y_{0}\) for some fixed values \(x_{0}\) and \(y_{0}\). A differential equation with an initial condition is called an initial value problem.
Example 1
Solve \(\frac{dy}{dx}=4x^7\) subject to the initial condition \(y(0) = 4\).
Solution First, find the general antiderivative:
\[ y(x) = \int 4x^7dx = \frac{1}{2}x^8 + C \]
Then choose \(C\) so that the initial condition is satisfied: \(y(0) = 0 + C = 4\). This yields \(C = 4\), and our solution is \(y = \frac{1}{2}x^8+4\).
Example 2
Solve the initial value problem \(\frac{dy}{dt}=\sin(\pi t)\), \(y(2) = 2\).
Solution First find the general antiderivative:
\[ y(t) = \int\sin(\pi t)dt = -\frac{1}{\pi}\cos(\pi t) + C \]
Then solve for \(C\) by evaluating at \(t = 2\):
\[ y(2) = -\frac{1}{\pi}\cos(2\pi) + C=2\implies C = 2 +\frac{1}{\pi} \]
The solution of the initial value problem is \(y(t)=-\frac{1}{\pi}\cos(\pi t) + 2 +\frac{1}{\pi}\).
Example 3
A car traveling with velocity \(24\text{ m/s}\) begins to slow down at time \(t = 0\) with a constant deceleration of \(a = -6\text{ m/s}^{2}\). Find
(a) the velocity \(v(t)\) at time \(t\), and
(b) the distance traveled before the car comes to a halt.
Solution
(a) The derivative of velocity is acceleration, so velocity is the antiderivative of acceleration:
Relation between position, velocity, and acceleration:
\begin{align*} s'(t)&=v(t)&s(t)&=\int v(t)dt\\ v'(t)&=a(t)&v(t)&=\int a(t)dt \end{align*}
\[ v(t) = \int adt = \int(-6)dt=-6t+C \]
The initial condition \(v(0) = C = 24\) gives us \(v(t) = -6t + 24\).
(b) Position is the antiderivative of velocity, so the car’s position is
\[ s(t) = \int v(t)dt = \int(-6t+24)dt = -3t^2+24t+C_1 \]
280
where \(C_{1}\) is a constant. We are not told where the car is at \(t = 0\), so let us set \(s(0) = 0\) for convenience, getting \(C_{1} = 0\). With this choice, \(s(t) = -3t^{2} + 24t\). This is the distance traveled from time \(t = 0\).
The car comes to a halt when its velocity is zero, so we solve
\[ v(t) = -6t+24 = 0\implies t=4\text{ s} \]
The distance traveled before coming to a halt is \(s(4) = -3(4^{2}) + 24(4) = 48\text{ m}\).
Let s(t) be the position at time t of an object in linear motion. Then the object’s velocity is v(t) = s′(t), and the integral of v(t) is equal to the net change in position or displacement over a time interval [t1, t2]:
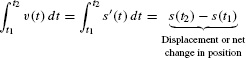
We must distinguish between displacement and distance traveled. If you travel 10 km and return to your starting point, your displacement is zero but your distance traveled is 20 km. To compute distance traveled rather than displacement, integrate the speed |v(t)|.
THEOREM 1 The Integral of Velocity
For an object in linear motion with velocity v(t), then
EXAMPLE 4
A particle has velocity v(t) = t3 −10t2 + 24t m/s. Compute:
- (a) Displacement over [0, 6]
- (b) Total distance traveled over [0, 6]
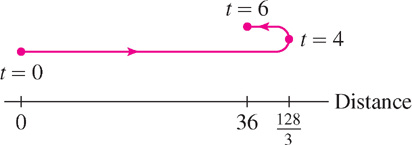
Indicate the particle’s trajectory with a motion diagram.
Solution First, we compute the indefinite integral:
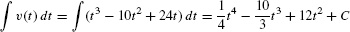
- (a) The displacement over the time interval [0, 6] is
- (b) The factorization v(t) = t(t − 4)(t − 6) shows that v(t) changes sign at t = 4. It is positive on [0, 4] and negative on [4, 6] as we see in Figure 6.44. Therefore, the total distance traveled is
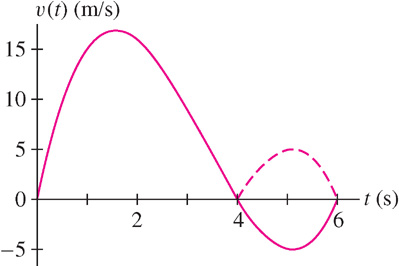Figure 6.44: Graph of v(t) = t3 − 10t2 + 24t. Over [4, 6], the dashed curve is the graph of |v(t)|.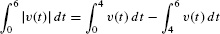
We evaluate these two integrals separately:
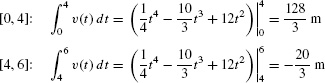
The total distance traveled is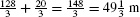 
Figure 6.45 is a motion diagram indicating the particle’s trajectory. The particle travels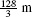 
during the first 4 s and then backtracks 
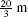over the next 2 s.
Question 6.12 Velocity and Distance Progress Check Question 1
o9jrGLxAhXC4jxMtlRWVQcQUiWohJqeAiOlz88CQGJSzhMUa8LkWog/3Jqll7gVN2Sh4y5VuffHVF4CRABsYliHECGFR3peVLoBsit16GjU4Cdi+zb1BGtvGNnuYcjANl5m01Ak89xKZDr43Eu3LHrGRcooIJydh0CLjnDoWzO4nBNvctkrL+p67DEiS8PLshnEWk68RiPi2Gpk3kITfp2k/UTp7aG2R/2yUkg3rXabMnwfnDjuEp48kn2US9as1dca8jDtRAww=Question 6.13 Velocity and Distance Progress Check Question 2
UbJt4kUVlkgKclo7h1Yo5HL94Je8c0HrR9El2oD8UG+/oEaP6wcGYVWNL7ip/LxnDvi0PZraeIA3A2juB5u7UNTsqpBrwf/fXNlsNxkg4jRunq/Ypjp0K4DR0DkICos+hdxyOV5UBE8kxK77LaUxQ7r1izXeAjUMx66vuWwZ90MfmSshG7zy6gIMNy2OApCs9LYm7f5qeCYzWcTthtStN22iyZ/E5HpzSnRfCjVKyocRGtIVfGc6Dl/UsaQP0P/Bt3NvvP9gkjU=6.5.2 Work and Energy
“For those who want some proof that physicists are human, the proof is in the idiocy of all the different units which they use for measuring energy.”
—Richard Feynman,
The Character of Physical Law
All physical tasks, from running up a hill to turning on a computer, require an expenditure of energy. When a force is applied to an object to move it, the energy expended is called work. When a constant force \(F\) is applied to move the object a distance \(d\) in the direction of the force, the work \(W\) is defined as “force times distance” (Figure 6.46): \[ \begin{equation} \boxed{\bbox[#FAF8ED,5pt]{W = F\cdot d}}\tag {1} \end{equation} \] The SI unit of force is the newton (abbreviated N), defined as \(1 \textrm{kg-m}\text{/}\mathrm{s}^2\). Energy and work are both measured in units of the joule (J), equal to 1 N-m. In the British system, the unit of force is the pound, and both energy and work are measured in foot-pounds (ft-lb). Another unit of energy is the calorie. One ft-lb is approximately 0.738 J or 3.088 calories.
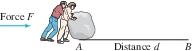
To become familiar with the units, let's calculate the work \(W\) required to lift a 2-kg stone 3 m above the ground. Gravity pulls down on the stone of mass \(m\) with a force equal to \(-mg\), where \(g = 9.8 \mathrm{m\text{/}s}^2\). Therefore, lifting the stone requires an upward vertical force \(F=mg\), and the work expended is \[ W = \underbrace{ (mg) h}_{F\,\cdot\, d} = (2 \mathrm{kg})(9.8 \mathrm{m\text{/}s}^2)(3 \mathrm{m}) = 58.8 \mathrm{J} \] The kilogram is a unit of mass, but the pound is a unit of force. Therefore, the factor \(g\) does not appear when work against gravity is computed in the British system. The work required to lift a 2-lb stone 3 ft is \[ W = \underbrace{(2 \mathrm{lb})(3 \mathrm{ft})}_{F\,\cdot\, d} = 6 \textrm{ft-lb} \]
We are interested in the case where the force \(F(x)\) varies as the object moves from \(a\) to \(b\) along the \(x\)-axis. Eq. (1) does not apply directly, but we can break up the task into a large number of smaller tasks for which Eq. (1) gives a good approximation. Divide \([a,b]\) into \(N\) subintervals of length \(\Delta x = ({b-a})/{N}\) as in Figure 6.47 and let \(W_i\) be the work required to move the object from \(x_{i-1}\) to \(x_i\). If \(\Delta x\) is small, then the force \(F(x)\) is nearly constant on the interval \([x_{i-1}, x_i]\) with value \(F(x_i)\), so \(W_i\approx F(x_i)\Delta x\). Summing the contributions, we obtain \[ W = \sum_{i=1}^N W_i \approx \underbrace{\sum_{i=1}^N F(x_i)\Delta x}_{\textrm{Right-endpoint approximation}} \] The sum on the right is a right-endpoint approximation that converges to \(\int_a^b F(x)\, dx\). This leads to the following definition.
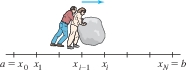
DEFINITION Work
The work performed in moving an object along the \(x\)-axis from \(a\) to \(b\) by applying a force of magnitude \(F(x)\) is \[ \begin{equation} \boxed{\bbox[#FAF8ED,5pt]{W = \int_a^b F(x)\, dx}}\tag {2} \end{equation} \]
392
One typical calculation involves finding the work required to stretch a spring. Assume that the free end of the spring has position \(x = 0\) at equilibrium, when no force is acting (Figure 6.48). According to Hooke's Law, when the spring is stretched (or compressed) to position \(x\), it exerts a restoring force of magnitude \(-kx\) in the opposite direction, where \(k\) is the spring constant. If we want to stretch the spring further, we must apply a force \(F(x) = kx\) to counteract the force exerted by the spring.
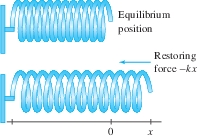
EXAMPLE 5 Hooke's Law
Assuming a spring constant of \(k = 400 \mathrm{N\text{/}m}\), find the work required to
- Stretch the spring 10 cm beyond equilibrium.
- Compress the spring 2 cm more when it is already compressed 3 cm.
Hooke's Law is named after the English scientist, inventor, and architect Robert Hooke (1635–1703), who made important discoveries in physics, astronomy, chemistry, and biology. He was a pioneer in the use of the microscope to study organisms. Unfortunately, Hooke was involved in several bitter disputes with other scientists, most notably with his contemporary Isaac Newton. Newton was furious when Hooke criticized his work on optics. Later, Hooke told Newton that he believed Kepler's Laws would follow from an inverse square law of gravitation, but Newton refused to acknowledge Hooke's contributions in his masterwork Principia. Shortly before his death in 1955, Albert Einstein commented on Newton's behavior: “That, alas, is vanity. You find it in so many scientists... it has always hurt me to think that Galileo did not acknowledge the work of Kepler”.
Solution A force \(F(x) = 400x\) N is required to stretch the spring (with \(x\) in meters). Note that centimeters must be converted to meters.
- The work required to stretch the spring 10 cm (0.1 m) beyond equilibrium is \[ W = \int_{0}^{0.1} 400x\, dx = 200x^2 \Big|_0^{0.1} = 2 \textrm{J} \]
- If the spring is at position \(x=-3\) cm, then the work \(W\) required to compress it further to \(x=-5\) cm is \[ W = \int_{-0.03}^{-0.05} 400x\, dx = 200x^2 \Big|_{-0.03}^{-0.05} = 0.5 - 0.18 = 0.32 \textrm{J} \] Observe that we integrate from the starting point \(x=-0.03\) to the ending point \(x= -0.05\) (even though the lower limit of the integral is larger than the upper limit in this case).
Question 6.14 Work and Energy Progress Check Question 1
98erWF+7sAhaOXahEjHMj0l+PI81v0pZN7lqwOeNNvPI/MPjFrJ8gOerA9g3+WVGl3Vq2rMY8/dzmnxA0b+0zcVLZjVtDCO8RJDnlnvalZdteID6JIg3EJUz8I1PMZG7ZRNLAOUGcC6m8SdRaTMBDjiBhfW0PF7Xllj8YFuTl07HPeUMyE28zh6ShfwE3/brg/FXbiUrDhz5tdKjKNeffFqAS3XL7UvK7CNGOMsqiyZ2EQcUNRftf7XEGcWr/y2+kjScIXYi6R5uqCVIzFyJFMmLYfP8ZNH3bQpQINJtlzMG3rPArRsGchHec4mZ2fPSvLeupUPhNj2quAb+ud4Xdy/llBlvZRaE7I1rnP/h+ioNtMNBvo+fcfD136eHgxFOGf6QoRsItkgbbs2XH4umlg==In the next two examples, we are not moving a single object through a fixed distance, so we cannot apply Eq. (2). Rather, each thin layer of the object is moved through a different distance. The work performed is computed by “summing” (i.e., integrating) the work performed on the thin layers.
On the earth's surface, work against gravity is equal to the force \(mg\) times the vertical distance through which the object is lifted. No work against gravity is done when an object is moved sideways.
EXAMPLE 6 Building a Cement Column
Compute the work (against gravity) required to build a cement column of height 5 m and square base of side 2 m. Assume that cement has density \(1500 \mathrm{kg\text{/}m}^{3}\).
Solution Think of the column as a stack of \(n\) thin layers of width \(\Delta y = 5/n\). The work consists of lifting up these layers and placing them on the stack (Figure 6.49), but the work performed on a given layer depends on how high we lift it.
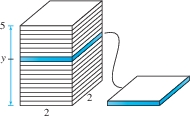
First, let us compute the gravitational force on a thin layer of width \(\Delta y\): \[ \begin{eqnarray} &\textrm{Volume of layer}& &=\textrm{area \(\times\) width} & &= 4\Delta y \textrm{m}^3\notag\\ &\textrm{Mass of layer}& &=\textrm{density \(\times\) volume} & &= 1500\cdot 4\Delta y \textrm{kg}\notag\\ &\textrm{Force on layer}& &= g \times \mathrm{mass} & &= 9.8\cdot 1500\cdot 4\Delta y=58{,}800\,\Delta y \textrm{N}\notag \end{eqnarray} \] The work performed in lifting this layer to height \(y\) is equal to the force times the distance \(y\), which is \((58{,}800\Delta y)y\). Setting \(L(y) = 58{,}800y\), we have \[ \boxed{\bbox[#FAF8ED,5pt]{ \textrm{Work lifting layer to height \(y\)} \approx (58{,}800\Delta y)y = L(y)\Delta y}} \]
393
This is only an approximation (although a very good one if \(\Delta y\) is small) because the layer has nonzero width and the cement particles at the top have been lifted a little bit higher than those at the bottom. The \(i\)th layer is lifted to height \(y_i\), so the total work performed is \[ W \approx \sum_{i=1}^n L(y_i)\,\Delta y \] This sum is a right-endpoint approximation to \(\int_0^5 L(y)\, dy\). Letting \(n\to\infty\), we obtain \[ W=\int_0^5 L(y)\, dy=\int_0^5 58{,}800 y\, dy = 58{,}800\frac{y^2}{2}\bigg|_0^5 = 735{,}000 \textrm{J} \]
In Examples 6 and 7, the work performed on a thin layer is written \[ L(y)\Delta y \] When we take the sum and let \(\Delta y\) approach zero, we obtain the integral of \(L(y)\). Symbolically, the \(\Delta y\) “becomes” the \(dy\) of the integral. Note that \[ \begin{align*} L(y) = g \;\times&\; density \times A(y)\\ &\times (vertical~distance~lifted) \end{align*} \] where \(A(y)\) is the area of the cross section.
EXAMPLE 7 Pumping Water out of a Tank
A spherical tank of radius \(R\) meters is filled with water. Calculate the work \(W\) performed (against gravity) in pumping out the water through a small hole at the top. The density of water is \(1000 \mathrm{kg\text{/}m}^3\).
Solution The first step, as in the previous example, is to compute the work against gravity performed on a thin layer of water of width \(\Delta y\). We place the origin of our coordinate system at the center of the sphere because this leads to a simple formula for the radius \(r\) of the cross section at height \(y\) (Figure 6.50).
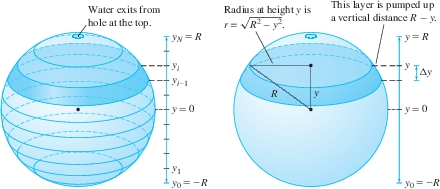
Step 1. Compute work performed on a layer.
Figure 6.50 shows that the cross section at height \(y\) is a circle of radius \(r = \sqrt{R^2-y^2}\) and area \(A(y) = \pi r^2 = \pi(R^2 - y^2)\). A thin layer has volume \(A(y)\Delta y\), and to lift it, we must exert a force against gravity equal to \[ \begin{alignat*}{2} \textrm{Force on layer}& = g \times \overbrace{\textrm{density}\times A(y)\Delta y}^{\textrm{mass}}&&\approx (9.8) 1000\pi(R^2 - y^2) \Delta y \end{alignat*} \] The layer has to be lifted a vertical distance \(R-y\), so \[ \begin{align*} \boxed{\bbox[#FAF8ED,5pt]{ \textrm{Work on layer} \approx \overbrace{9800\pi(R^2 - y^2)\Delta y}^{\textrm{Force against gravity}}\,\,\, \times \overbrace{(R-y)}^{\textrm{Vertical distance lifted}} = L(y)\Delta y}} \end{align*} \] where \(L(y)=9800\pi(R^3-R^2y -Ry^2+y^3)\).
Step 2. Compute total work.
Now divide the sphere into \(N\) layers and let \(y_i\) be the height of the \(i\)th layer. The work performed on \(i\)th layer is approximately \(L(y_i)\,\Delta y\), and therefore \[ W \approx \sum_{i=1}^N L(y_i),\Delta y \]
394
This sum approaches the integral of \(L(y)\) as \(N\to \infty\) (that is, \(\Delta y \to 0\)), so \[ \begin{align} W &= \int_{-R}^RL(y)\,dy =9800\pi\int_{-R}^R(R^3-R^2y -Ry^2+y^3)\,dy\notag\\ & = 9800\pi \left(R^3y-\frac12R^2y^2-\frac13Ry^3+\frac14y^4 \right)\bigg|_{-R}^R = \frac{39{,}200\pi}3\,R^4 \textrm{J}\notag \end{align} \] Note that the integral extends from \(-R\) to \(R\) because the \(y\)-coordinate along the sphere varies from \(-R\) to \(R\).
A liter of gasoline has an energy content of approximately \(3.4\times 10^7\) joules. The previous example shows that the work required to pump water out of a sphere of radius \(R=5\) meters is \[ W = \left(\frac{39{,}200\pi}3\right)5^4\approx 2.6\times 10^7\,\,\textrm{J} \] or the energy content of roughly three-fourths of a liter of gasoline.
6.5.3 Summary
- For an object traveling in a straight line at velocity v(t),
- Work performed to move an object: \[ \textrm{Constant force:}\quad W = F\cdot d,\qquad \textrm{Variable force:}\quad W = \int_a^b F(x)\, dx \]
- Hooke's Law: A spring stretched \(x\) units past equilibrium exerts a restoring force of magnitude \(-kx\). A force \(F(x) = kx\) is required to stretch the spring further.
- To compute work against gravity by decomposing an object into \(N\) thin layers of thickness \(\Delta y\), express the work performed on a thin layer as \(L(y)\Delta y\), where \[ L(y) = g \times\textrm{density}\times A(y) \times \textrm{(vertical distance lifted)} \] The total work performed is \(\displaystyle W = \int_a^b L(y)\,dy\).